NCERT Solutions for Class 8 Maths Chapter 8 Algebraic Expressions and Identities (Updated Pattern)

In earlier classes, we have already become familiar with what algebraic expressions
(or simply expressions) are. Examples of expressions are:

1. Expressions are formed from variables and constants.

2. Terms are added to form expressions. Terms themselves are formed as a product of factors.
3. Expressions that contain exactly one, two and three terms are called monomials, binomials and trinomials respectively. In general, any expression containing one or more terms with non-zero coefficients (and with variables having non-negative integers as exponents) is called a polynomial.
4. Like terms are formed from the same variables and the powers of these variables are the same, too. Coefficients of like terms need not be the same.
5. While adding (or subtracting) polynomials, first look for like terms and add (or subtract) them; then handle the unlike terms.
6. There are several situations in which we need to multiply algebraic expressions: for example, in finding the area of a rectangle, the sides of which are given as expressions.
7. A monomial multiplied by a monomial always gives a monomial.
8. While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the monomial.
9. In carrying out the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term, i.e., every term of the polynomial is multiplied by every term in the binomial (or trinomial).
   Note that in such multiplication, we may get terms in the product which are like and have to be combined.

——————–Exercise 8.1———————–

1. Add the following.

(i) ab – bc, bc – ca, ca – ab

(ii) a – b + ab, b – c + bc, c – a + ac

(iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²

(iv) l² + m², m² + n², n² + l², 2lm + 2mn + 2nl

Solution:

i) (ab – bc) + (bc – ca) + (ca-ab)

= ab – bc + bc – ca + ca – ab

= ab – ab – bc + bc – ca + ca

= 0

ii) (a – b + ab) + (b – c + bc) + (c – a + ac)

= a – b + ab + b – c + bc + c – a + ac

= a – a +b – b +c – c + ab + bc + ca

= 0 + 0 + 0 + ab + bc + ca

= ab + bc + ca

iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²

= (2p²q² – 3pq + 4) + (5 + 7pq – 3p²q²)

= 2p²q² – 3p²q² – 3pq + 7pq + 4 + 5

= – p²q² + 4pq + 9

NCERT Solutions for Class 8 Maths Chapter 7 Comparing Quantities (Updated Pattern)

iv)(l² + m²) + (m² + n²) + (n² + l²) + (2lm + 2mn + 2nl)

= l² + l² + m² + m² + n² + n² + 2lm + 2mn + 2nl

= 2l² + 2m² + 2n² + 2lm + 2mn + 2nl

2. (a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3

(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz

 (c) Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq² + 5p²q

Solution:

(a) (12a – 9ab + 5b – 3) – (4a – 7ab + 3b + 12)

= 12a – 9ab + 5b – 3 – 4a + 7ab – 3b – 12

= 12a – 4a -9ab + 7ab +5b – 3b -3 -12

= 8a – 2ab + 2b – 15

b) (5xy – 2yz – 2zx + 10xyz) – (3xy + 5yz – 7zx)

= 5xy – 2yz – 2zx + 10xyz – 3xy – 5yz + 7zx

=5xy – 3xy – 2yz – 5yz – 2zx + 7zx + 10xyz

= 2xy – 7yz + 5zx + 10xyz

c) (18 – 3p – 11q + 5pq – 2pq² + 5p²q) – (4p²q – 3pq + 5pq² – 8p + 7q – 10)

= 18 – 3p – 11q + 5pq – 2pq² + 5p²q – 4p²q + 3pq – 5pq² + 8p – 7q + 10

= 28 + 5p – 18q + 8pq – 7pq² + p²q

——————–Exercise 8.2———————–

1. Find the product of the following pairs of monomials.

(i) 4, 7p

(ii) – 4p, 7p

(iii) – 4p, 7pq

(iv)  4p³, – 3p

(v) 4p, 0

Solution:

(i) 4 , 7 p =  4 × 7 × p = 28p

(ii) – 4p × 7p = (-4 × 7 ) × (p × p )= -28p²

(iii) – 4p × 7pq =(-4 × 7 ) (p × pq) =  -28p²q

(iv) 4p³ × – 3p = (4 × -3 ) (p³ × p ) =  -12p⁴

(v) 4p ×  0 = 0

2. Find the areas of rectangles with the following pairs of monomials as their lengths and breadths, respectively.

(p, q) ; (10m, 5n) ; (20x² , 5y²) ; (4x, 3x²) ; (3mn, 4np)

Solution:

Area of rectangle = Length x breadth. So, it is the multiplication of two monomials.

The results can be written in square units.

(i) p × q = pq

(ii)10m ×  5n = 50mn

(iii) 20x² ×  5y² =  100x²y²

(iv) 4x × 3x² = 12x³

(v) 3mn ×  4np = 12mn²p

The Secret of Padmasana: Unlocking Meditation and Inner Balance with the Lotus Pose

3. Complete the following table of products:

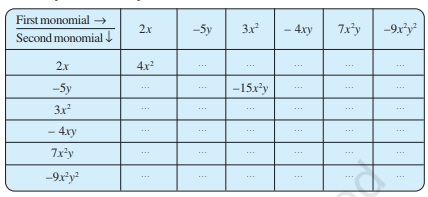
Solution:

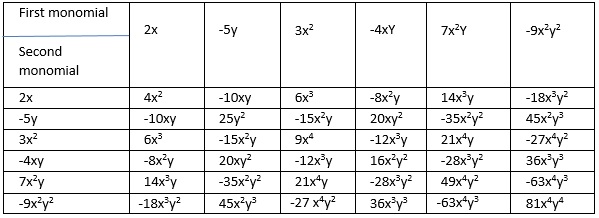
4. Obtain the volume of rectangular boxes with the following length, breadth and height, respectively.

(i) 5a, 3a², 7a⁴

(ii) 2p, 4q, 8r

(iii) xy, 2x²y, 2xy²

(iv) a, 2b, 3c

Solution:

The volume of the rectangle = length x  breadth x  height. To evaluate the volume of rectangular boxes, multiply all the monomials.

(i) 5a x 3a² x 7a⁴ = (5 × 3 × 7) (a × a² × a⁴ ) = 105a⁷

(ii) 2p x 4q x 8r = (2 × 4 × 8 ) (p × q × r ) = 64pqr

(iii) y × 2x²y × 2xy² =(1 × 2 × 2 )( x × x² × x × y × y × y² ) =  4x⁴y⁴

(iv) a x  2b x 3c = (1 × 2 × 3 ) (a × b × c) = 6abc

5. Obtain the product of

(i) xy,  yz, zx

(ii) a, – a² , a³

(iii) 2, 4y, 8y² , 16y³

(iv) a, 2b, 3c, 6abc

(v) m, – mn, mnp

Solution:

(i) xy × yz × zx = x² y² z²

(ii) a × – a²  × a³ = – a⁶

(iii) 2 × 4y × 8y² × 16y³ = 1024 y⁶

(iv) a × 2b × 3c × 6abc = 36a² b² c²

(v) m × – mn × mnp = –m³ n² p

——————–Exercise 8.3———————–

1. Carry out the multiplication of the expressions in each of the following pairs.

(i) 4p, q + r

(ii) ab, a – b

(iii) a + b, 7a²b²

(iv) a² – 9, 4a

(v) pq + qr + rp, 0

Solution:

(i)4p(q + r) = 4pq + 4pr

(ii)ab(a – b) = a² b – a b²

(iii)(a + b) (7a²b²) = 7a³b² + 7a²b³

(iv) (a² – 9)(4a) = 4a³ – 36a

(v) (pq + qr + rp) × 0 = 0 ( Anything multiplied by zero is zero )

2. Complete the table.

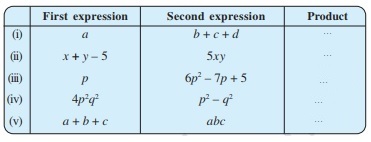
Solution:

	First expression	Second expression	Product
(i)	a	b + c + d	a(b+c+d)= a×b + a×c + a×d= ab + ac + ad
(ii)	x + y – 5	5xy	5 xy (x + y – 5)= 5 xy x x + 5 xy x y – 5 xy x 5= 5 x2y + 5 xy2 – 25xy
(iii)	p	6p2 – 7p + 5	p (6 p 2-7 p +5)= p× 6 p2 – p× 7 p + p×5= 6 p3 – 7 p2 + 5 p
(iv)	4 p2 q2	P2 – q2	4p2 q2 * (p2 – q2 )=4 p4 q2– 4p2 q4
(v)	a + b + c	abc	abc(a + b + c)= abc × a + abc × b + abc × c= a2bc + ab2c + abc2

3. Find the product.

i) a² x (2a²²) x (4a²⁶)

ii) (2/3 xy) ×(-9/10 x²y²)

(iii) (-10/3 pq³/) × (6/5 p³q)

(iv) (x) × (x²) × (x³) × (x⁴)

Solution:

i) a² x (2a²²) x (4a²⁶)

= (2 × 4) ( a² × a²² × a²⁶ )

= 8 × a^{2 + 22 + 26} 

= 8a⁵⁰

ii) (2xy/3) ×(-9x²y²/10)

=(2/3 × -9/10 ) ( x × x² × y × y² )

= (-3/5 x³y³)

iii) (-10pq³/3) ×(6p³q/5)

= ( -10/3 × 6/5 ) (p × p³× q³ × q)

= (-4p⁴q⁴)

iv)  ( x) x (x²) x (x³) x (x⁴)

= x ^{1 + 2 + 3 + 4} 

=  x¹⁰

4. (a) Simplify 3x (4x – 5) + 3 and find its values for (i) x = 3 (ii) x =1/2

(b) Simplify a (a²+ a + 1) + 5 and find its value for (i) a = 0, (ii) a = 1 (iii) a = – 1.

Solution:

a) 3x (4x – 5) + 3

=3x ( 4x) – 3x( 5) +3

=12x² – 15x + 3

(i) Putting x=3 in the equation we gets 12x² – 15x + 3 =12(3²) – 15 (3) +3

= 108 – 45 + 3

= 66

(ii) Putting x=1/2 in the equation we get

12x² – 15x + 3 = 12 (1/2)² – 15 (1/2) + 3

= 12 (1/4) – 15/2 +3

= 3 – 15/2 + 3

= 6- 15/2

= (12- 15 ) /2

= -3/2

b) a(a² +a +1)+5

= a x a² + a x a + a x 1 + 5 =a³+a²+a+ 5

(i) putting a=0 in the equation we get 0³+0²+0+5=5

(ii) putting a=1 in the equation we get 1³ + 1² + 1+5 = 1 + 1 + 1+5 = 8

(iii) Putting a = -1 in the equation we get (-1)³+(-1)² + (-1)+5 = -1 + 1 – 1+5 = 4

5. (a) Add: p ( p – q), q ( q – r) and r ( r – p) 

(b) Add: 2x (z – x – y) and 2y (z – y – x) 

(c) Subtract: 3l (l – 4 m + 5 n) from 4l ( 10 n – 3 m + 2 l ) 

(d) Subtract: 3a (a + b + c ) – 2 b (a – b + c)  from 4c ( – a + b + c )

Solution:

a) p ( p – q) + q ( q – r) + r ( r – p)

= (p² – pq) + (q² – qr) + (r² – pr)

= p² + q² + r² – pq – qr – pr

b) 2x (z – x – y) + 2y (z – y – x)

= (2xz – 2x² – 2xy) + (2yz – 2y² – 2xy)

= 2xz – 4xy + 2yz – 2x² – 2y²

c) 4l ( 10 n – 3 m + 2 l ) – 3l (l – 4 m + 5 n)

= (40ln – 12lm + 8l²) – (3l² – 12lm + 15ln)

= 40ln – 12lm + 8l² – 3l² +12lm -15 ln

= 25 ln + 5l²

d) 4c ( – a + b + c ) – (3a (a + b + c ) – 2 b (a – b + c))

= (-4ac + 4bc + 4c²) – (3a² + 3ab + 3ac – ( 2ab – 2b² + 2bc ))

=-4ac + 4bc + 4c² – (3a² + 3ab + 3ac – 2ab + 2b² – 2bc)

= -4ac + 4bc + 4c² – 3a² – 3ab – 3ac +2ab – 2b² + 2bc

= -7ac + 6bc + 4c² – 3a² – ab – 2b²

——————–Exercise 8.4———————–

1. Multiply the binomials.

(i) (2x + 5) and (4x – 3)

(ii) (y – 8) and (3y – 4)

(iii) (2.5l – 0.5m) and (2.5l + 0.5m)

(iv) (a + 3b) and (x + 5)

(v) (2pq + 3q²) and (3pq – 2q²)

(vi) (3/4 a² + 3b²) and 4( a² – 2/3 b²)

Solution :

(i) (2x + 5)(4x – 3)

= 2x x 4x – 2x x 3 + 5 x 4x – 5 x 3

= 8x² – 6x + 20x -15

= 8x² + 14x -15

ii) ( y – 8)(3y – 4)

= y x 3y – 4y – 8 x 3y + 32

= 3y² – 4y – 24y + 32

= 3y² – 28y + 32

(iii) (2.5l – 0.5m)(2.5l + 0.5m)

= 2.5l x 2.5 l + 2.5l x 0.5m – 0.5m x 2.5l – 0.5m x 0.5m

= 6.25l² + 1.25 lm – 1.25 lm – 0.25 m²

= 6.25l² – 0.25 m²

iv) (a + 3b) (x + 5)

= ax + 5a + 3bx + 15b

v) (2pq + 3q²) (3pq – 2q²)

= 2pq x 3pq – 2pq x 2q² + 3q² x 3pq – 3q² x 2q²

= 6p²q² – 4pq³ + 9pq³ – 6q⁴

= 6p²q² + 5pq³ – 6q⁴

(vi) (3/4 a² + 3b² ) and 4( a² – 2/3 b² )

=(3/4 a² + 3b² ) x 4( a² – 2/3 b² )

=(3/4 a² + 3b² ) x (4a² – 8/3 b² )

=3/4 a² x (4a² – 8/3 b² ) + 3b² x (4a² – 8/3 b² )

=3/4 a² x 4a² -3/4 a² x 8/3 b² + 3b² x 4a² – 3b² x 8/3 b²

=3a⁴– 2a² b² + 12 a²  b² – 8b⁴

= 3a⁴ + 10a²  b² – 8b⁴

2. Find the product.

(i) (5 – 2x) (3 + x)

(ii) (x + 7y) (7x – y)

(iii) (a²+ b) (a + b²)

(iv) (p² – q²) (2p + q)

Solution:

(i) (5 – 2x) (3 + x)

= 5 (3 + x) – 2x (3 + x)

=15 + 5x – 6x – 2x²

= 15 – x -2 x ²

(ii) (x + 7y) (7x – y)

= x(7x-y) + 7y ( 7x-y)

=7x² – xy + 49xy – 7y²

= 7x² – 7y² + 48xy

iii) (a²+ b) (a + b²)

= a²  (a + b²) + b(a + b²)

= a³ + a²b² + ab + b³

= a³ + b³ + a²b² + ab

iv) (p²– q²) (2p + q)

= p² (2p + q) – q² (2p + q)

=2p³ + p²q – 2pq² – q³

= 2p³ – q³ + p²q – 2pq²

3. Simplify.

(i) (x²– 5) (x + 5) + 25

(ii) (a²+ 5) (b³+ 3) + 5

(iii)(t + s²)(t² – s)

(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)

(v) (x + y)(2x + y) + (x + 2y)(x – y)

(vi) (x + y)(x²– xy + y²)

(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y

(viii) (a + b + c)(a + b – c)

Solution:

i) (x²– 5) (x + 5) + 25

= x³ + 5x² – 5x – 25 + 25

= x³ + 5x² – 5x

ii) (a²+ 5) (b³+ 3) + 5

= a²b³ + 3a² + 5b³ + 15 + 5

= a²b³ + 5b³ + 3a² + 20

iii) (t + s²)(t² – s)

= t (t² – s) + s²(t² – s)

= t³ – st + s²t² – s³

= t³ – s³ – st + s²t²

iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)

= (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)

=(ac – ad + bc – bd) + (ac + ad – bc – bd) + (2ac + 2bd)

= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd

= 4ac

v) (x + y)(2x + y) + (x + 2y)(x – y)

= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²

= 3x² + 4xy – y²

vi) (x + y)(x²– xy + y²)

= x³ – x²y + xy² + x²y – xy² + y³

= x³ + y³

vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y

= 2.25x² + 6xy + 4.5x – 6xy – 16y² – 12y – 4.5x + 12y = 2.25x² – 16y²

viii) (a + b + c)(a + b – c)

= a² + ab – ac + ab + b² – bc + ac + bc – c²

= a² + b² – c² + 2ab