
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals are given here. Students can either practise online or download these files and practise different types of questions related to this chapter, and achieve maximum marks in their examinations. Students have learnt addition and subtraction of fractions and addition and subtraction of decimals in earlier classes. In this class, students shall learn about multiplication and division of fractions and multiplication and division of decimals.
Exercise 2.1 Page: 31
1. Solve:
(i) 2 – (3/5)
Solution:-
For subtraction of two, unlike fractions, first, change them to like fractions.
LCM of 1, 5 = 5
Now, let us change each of the given fractions into an equivalent fraction having 5 as the denominator.
= [(2/1) × (5/5)] = (10/5)
= [(3/5) × (1/1)] = (3/5)
Now,
= (10/5) – (3/5)
= [(10 – 3)/5]
= (7/5)
(ii) 4 + (7/8)
Solution:-
For the addition of two unlike fractions, first change them to like fractions.
LCM of 1, 8 = 8
Now, let us change each of the given fractions into an equivalent fraction having 8 as the denominator.
= [(4/1) × (8/8)] = (32/8)
= [(7/8) × (1/1)] = (7/8)
Now,
= (32/8) + (7/8)
= [(32 + 7)/8]
= (39/8)
=
(iii) (3/5) + (2/7)
Solution:-
For the addition of two unlike fractions, first change them to like fractions.
LCM of 5, 7 = 35
Now, let us change each of the given fractions into an equivalent fraction having 35 as the denominator.
= [(3/5) × (7/7)] = (21/35)
= [(2/7) × (5/5)] = (10/35)
Now,
= (21/35) + (10/35)
= [(21 + 10)/35]
= (31/35)
(iv) (9/11) – (4/15)
Solution:-
For subtraction of two, unlike fractions, first, change them to like fractions.
LCM of 11, 15 = 165
Now, let us change each of the given fractions into an equivalent fraction having 165 as the denominator.
= [(9/11) × (15/15)] = (135/165)
= [(4/15) × (11/11)] = (44/165)
Now,
= (135/165) – (44/165)
= [(135 – 44)/165]
= (91/165)
(v) (7/10) + (2/5) + (3/2)
Solution:-
For the addition of two unlike fractions, first change them to like fractions.
LCM of 10, 5, 2 = 10
Now, let us change each of the given fractions into an equivalent fraction having 35 as the denominator.
= [(7/10) × (1/1)] = (7/10)
= [(2/5) × (2/2)] = (4/10)
= [(3/2) × (5/5)] = (15/10)
Now,
= (7/10) + (4/10) + (15/10)
= [(7 + 4 + 15)/10]
= (26/10)
= (13/5)
=
(vi)
Solution:-
First, convert mixed fractions into improper fractions,
=
= 3 ½ = 7/2
For the addition of two unlike fractions, first change them to like fractions.
LCM of 3, 2 = 6
Now, let us change each of the given fractions into an equivalent fraction having 6 as the denominator.
= [(8/3) × (2/2)] = (16/6)
= [(7/2) × (3/3)] = (21/6)
Now,
= (16/6) + (21/6)
= [(16 + 21)/6]
= (37/6)
=
(vii)
812−358
Solution:-
First, convert mixed fractions into improper fractions,
= 8 ½ = 17/2
=
For subtraction of two, unlike fractions, first, change them to like fractions.
LCM of 2, 8 = 8
Now, let us change each of the given fractions into an equivalent fraction having 35 as the denominator.
= [(17/2) × (4/4)] = (68/8)
= [(29/8) × (1/1)] = (29/8)
Now,
= (68/8) – (29/8)
= [(68 – 29)/8]
= (39/8)
=
2. Arrange the following in descending order:
(i) 2/9, 2/3, 8/21
Solution:-
LCM of 9, 3, 21 = 63
Now, let us change each of the given fractions into an equivalent fraction having 63 as the denominator.[(2/9) × (7/7)] = (14/63) [(2/3) × (21/21)] = (42/63) [(8/21) × (3/3)] = (24/63)
Clearly,
(42/63) > (24/63) > (14/63)
Hence,
(2/3) > (8/21) > (2/9)
Hence, the given fractions in descending order are (2/3), (8/21), (2/9)
(ii) 1/5, 3/7, 7/10
Solution:-
LCM of 5, 7, 10 = 70
Now, let us change each of the given fractions into an equivalent fraction having 70 as the denominator.[(1/5) × (14/14)] = (14/70) [(3/7) × (10/10)] = (30/70) [(7/10) × (7/7)] = (49/70)
Clearly,
(49/70) > (30/70) > (14/70)
Hence,
(7/10) > (3/7) > (1/5)
Hence, the given fractions in descending order are (7/10), (3/7), (1/5)
3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
| 4/11 | 9/11 | 2/11 |
| 3/11 | 5/11 | 7/11 |
| 8/11 | 1/11 | 6/11 |
Solution:-
Sum along the first row = (4/11) + (9/11) + (2/11) = (15/11)
Sum along the second row = (3/11) + (5/11) + (7/11) = (15/11)
Sum along the third row = (8/11) + (1/11) + (6/11) = (15/11)
Sum along the first column = (4/11) + (3/11) + (8/11) = (15/11)
Sum along the second column = (9/11) + (5/11) + (1/11) = (15/11)
Sum along the third column = (2/11) + (7/11) + (6/11) = (15/11)
Sum along the first diagonal = (4/11) + (5/11) + (6/11) = (15/11)
Sum along the second diagonal = (2/11) + (5/11) + (8/11) = (15/11)
Yes. The sum of the numbers in each row, in each column and along the diagonals is the same, so it is a magic square.
4. A rectangular sheet of paper is 12 ½ cm long and cm wide. Find its perimeter.
Solution:-
From the question, it is given that,
Length = 12 ½ cm = 25/2 cm
Breadth =
We know that,
Perimeter of the rectangle = 2 × (length + breadth)
= 2 × [(25/2) + (32/3)]
= 2 × {[(25 × 3) + (32 × 2)]/6}
= 2 × [(75 + 64)/6]
= 2 × [139/6]
= 139/3 cm
Hence, the perimeter of the sheet of paper is
5. Find the perimeters of (i) the triangle ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?
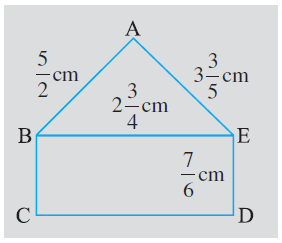
Solution:-
From the figure,
AB = (5/2) cm
AE =
BE =
ED = 7/6 cm
(i) We know that,
Perimeter of the triangle = Sum of all sides
Then,
The perimeter of triangle ABE = AB + BE + EA
= (5/2) + (11/4) + (18/5)
The LCM of 2, 4, 5 = 20
Now, let us change each of the given fractions into an equivalent fraction having 20 as the denominator.
= {[(5/2) × (10/10)] + [(11/4) × (5/5)] + [(18/5) × (4/4)]}
= (50/20) + (55/20) + (72/20)
= (50 + 55 + 72)/20
= 177/20
=
(ii) Now, we have to find the perimeter of the rectangle,
We know that,
Perimeter of the rectangle = 2 × (length + breadth)
Then,
Perimeter of rectangle BCDE = 2 × (BE + ED)
= 2 × [(11/4) + (7/6)]
The LCM of 4, 6 = 12
Now, let us change each of the given fractions into an equivalent fraction having 20 as the denominator
= 2 × {[(11/4) × (3/3)] + [(7/6) × (2/2)]}
= 2 × [(33/12) + (14/12)]
= 2 × [(33 + 14)/12]
= 2 × (47/12)
= 47/6
=
Finally, we have to find which one has a greater perimeter.
Perimeter of triangle ABE = (177/20)
Perimeter of rectangle BCDE = (47/6)
The two perimeters are in the form of unlike fractions.
Changing perimeters into like fractions we have,
(177/20) = (177/20) × (3/3) = 531/60
(43/6) = (43/6) × (10/10) = 430/60
Clearly, (531/60) > (430/60)
Hence, (177/20) > (43/6)
∴ Perimeter of Triangle ABE > Perimeter of Rectangle (BCDE)
6. Salil wants to put a picture in a frame. The picture is cm wide. To fit in the frame the picture cannot be more than cm wide. How much should the picture be trimmed?
Solution:-
From the question, it is given that,
Picture having a width of =
Frame having a width of =
∴ The picture should be trimmed by = [(38/5) – (73/10)]
The LCM of 5, 10 = 10
Now, let us change each of the given fractions into an equivalent fraction having 10 as the denominator.
= [(38/5) × (2/2)] – [(73/10) × (1/1)]
= (76/10) – (73/10)
= (76 – 73)/10
= 3/10 cm
Thus, the picture should be trimmed by (3/10) cm
7. Ritu ate (3/5) part of an apple and the remaining apple was eaten by her brother Somu. What part of the apple did Somu eat? Who had the larger share? By how much?
Solution:-
From the question, it is given that,
Part of the apple eaten by Ritu is = (3/5)
Part of the apple eaten by Somu is = 1 – Part of the apple eaten by Ritu
= 1 – (3/5)
The LCM of 1, 5 = 5
Now, let us change each of the given fractions into an equivalent fraction having 10 as the denominator.
= [(1/1) × (5/5)] – [(3/5) × (1/1)]
= (5/5) – (3/5)
= (5 – 3)/5
= 2/5
∴ Part of the apple eaten by Somu is (2/5)
So, (3/5) > (2/5) hence, Ritu ate a larger size of an apple.
Now, the difference between the 32 shares = (3/5) – (2/5)
= (3 – 2)/5
= 1/5
Thus, Ritu’s share is larger than the share of Somu by (1/5)
8. Michael finished colouring a picture in the (7/12) hour. Vaibhav finished colouring the same picture in (3/4) hour. Who worked longer? By what fraction was it longer?
Solution:-
From the question, it is given that,
The time taken by Michael to colour the picture is = (7/12)
The time taken by the Vaibhav to colour the picture is = (3/4)
The LCM of 12, 4 = 12
Now, let us change each of the given fractions into an equivalent fraction having 12 as the denominator.
(7/12) = (7/12) × (1/1) = 7/12
(3/4) = (3/4) × (3/3) = 9/12
Clearly, (7/12) < (9/12)
Hence, (7/12) < (3/4)
Thus, Vaibhav worked for a longer time.
So, Vaibhav worked longer time by = (3/4) – (7/12)
= (9/12) – (7/12)
= (9 – 7)/12
= (2/12)
= (1/6) of an hour.
Exercise 2.2 Page: 36
1. Which of the drawings (a) to (d) show:
(i) 2 × (1/5) (ii) 2 × ½ (iii) 3 × (2/3) (iv) 3 × ¼
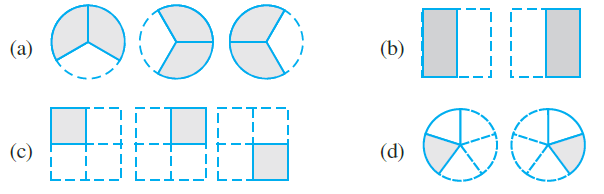
Solution:-
(i) 2 × (1/5) represents the addition of 2 figures, each representing 1 shaded part out of 5 equal parts.
∴ 2 × (1/5) is represented by fig (d).
(ii) 2 × ½ represents the addition of 2 figures, each representing 1 shaded part out of 2 equal parts.
∴ 2 × ½ is represented by fig (b).
(iii) 3 × (2/3) represents the addition of 3 figures, each representing 2 shaded parts out of 3 equal parts.
∴ 3 × (2/3) is represented by fig (a).
(iii) 3 × ¼ represents the addition of 3 figures, each representing 1 shaded part out of 4 equal parts.
∴ 3 × ¼ is represented by fig (c).
2. Some pictures (a) to (c) are given below. Tell which of them show:
(i) 3 × (1/5) = (3/5) (ii) 2 × (1/3) = (2/3) (iii) 3 × (3/4) = 2 ¼
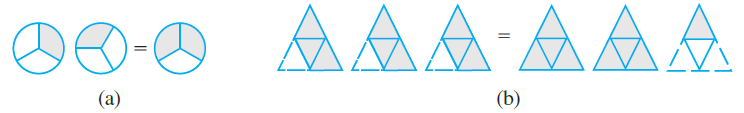

Solution:-
(i) 3 × (1/5) represents the addition of 3 figures, each representing 1 shaded part out of the given 5 equal parts and (3/5) represents 3 shaded parts out of 5 equal parts.
∴ 3 × (1/5) = (3/5) is represented by fig (c).
(ii) 2 × (1/3) represents the addition of 2 figures, each representing 1 shaded part out of the given 3 equal parts and (2/3) represents 2 shaded parts out of 3 equal parts.
∴ 2 × (1/3) = (2/3) is represented by fig (a).
(iii) 3 × (3/4) represents the addition of 3 figures, each representing 3 shaded parts out of the given 4 equal parts and 2 ¼ represents 2 fully and 1 figure having 1 part as shaded out of 4 equal parts.
∴ 3 × (3/4) = 2 ¼ is represented by fig (b).
3. Multiply and reduce to the lowest form and convert into a mixed fraction:
(i) 7 × (3/5)
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (7/1) × (3/5)
= (7 × 3)/ (1 × 5)
= (21/5)
=
(ii) 4 × (1/3)
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (4/1) × (1/3)
= (4 × 1)/ (1 × 3)
= (4/3)
=
(iii) 2 × (6/7)
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2/1) × (6/7)
= (2 × 6)/ (1 × 7)
= (12/7)
=
(iv) 5 × (2/9)
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/1) × (2/9)
= (5 × 2)/ (1 × 9)
= (10/9)
=
(v) (2/3) × 4
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2/3) × (4/1)
= (2 × 4)/ (3 × 1)
= (8/3)
=
(vi) (5/2) × 6
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/2) × (6/1)
= (5 × 6)/ (2 × 1)
= (30/2)
= 15
(vii) 11 × (4/7)
Solution:-
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (11/1) × (4/7)
= (11 × 4)/ (1 × 7)
= (44/7)
=
(viii) 20 × (4/5)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (20/1) × (4/5)
= (20 × 4)/ (1 × 5)
= (80/5)
= 16
(ix) 13 × (1/3)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (13/1) × (1/3)
= (13 × 1)/ (1 × 3)
= (13/3)
=
(x) 15 × (3/5)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (15/1) × (3/5)
= (15 × 3)/ (1 × 5)
= (45/5)
= 9
4. Shade:
(i) ½ of the circles in box (a) (b) 2/3 of the triangles in box (b)
(iii) 3/5 of the squares in the box (c)
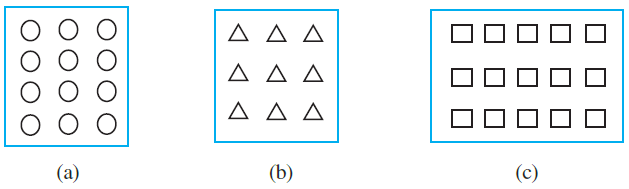
Solution:-
(i) From the question,
We may observe that there are 12 circles in the given box. So, we have to shade ½ of the circles in the box.
∴ 12 × ½ = 12/2
= 6
So we have to shade any 6 circles in the box.
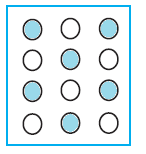
(ii) From the question,
We may observe that there are 9 triangles in the given box. So, we have to shade 2/3 of the triangles in the box.
∴ 9 × (2/3) = 18/3
= 6
So we have to shade any 6 triangles in the box.

(iii) From the question,
We may observe that there are 15 squares in the given box. So, we have to shade 3/5 of the squares in the box.
∴ 15 × (3/5) = 45/5
= 9
So we have to shade any 9 squares in the box.
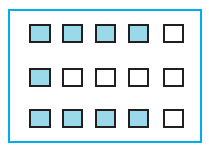
5. Find:
(a) ½ of (i) 24 (ii) 46
Solution:-
(i) 24
We have,
= ½ × 24
= 24/2
= 12
(ii) 46
We have,
= ½ × 46
= 46/2
= 23
(b) 2/3 of (i) 18 (ii) 27
Solution:-
(i) 18
We have,
= 2/3 × 18
= 2 × 6
= 12
(ii) 27
We have,
= 2/3 × 27
= 2 × 9
= 18
(c) ¾ of (i) 16 (ii) 36
Solution:-
(i) 16
We have,
= ¾ × 16
= 3 × 4
= 12
(ii) 36
We have
= ¾ × 36
= 3 × 9
= 27
(d) 4/5 of (i) 20 (ii) 35
Solution:-
(i) 20
We have,
= 4/5 × 20
= 4 × 4
= 16
(ii) 35
We have,
= 4/5 × 35
= 4 × 7
= 28
6. Multiply and express as a mixed fraction:
(a) 3 ×
Solution:-
First, convert the given mixed fraction into improper fraction.
=
Now,
= 3 × (26/5)
= 78/5
=
(b) 5 × 6 ¾
Solution:-
First convert the given mixed fraction into improper fraction.
= 6 ¾ = 27/4
Now,
= 5 × (27/4)
= 135/4
= 33 ¾
(c) 7 × 2 ¼
Solution:-
First convert the given mixed fraction into improper fraction.
= 2 ¼ = 9/4
Now,
= 7 × (9/4)
= 63/4
= 15 ¾
(d) 4 ×
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= 4 × (19/3)
= 76/3
=
(e) 3 ¼ × 6
Solution:-
First convert the given mixed fraction into improper fraction.
= 3 ¼ = 13/4
Now,
= (13/4) × 6
= (13/2) × 3
= 39/2
= 19 ½
(f) × 8
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (17/5) × 8
= 136/5
=
7. Find:
(a) ½ of (i) 2 ¾ (ii)
Solution:-
(i) 2 ¾
First convert the given mixed fraction into improper fraction.
= 2 ¾ = 11/4
Now,
= ½ × 11/4
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ½ × (11/4)
= (1 × 11)/ (2 × 4)
= (11/8)
=
(ii)
First convert the given mixed fraction into improper fraction.
=
Now,
= ½ × (38/9)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ½ × (38/9)
= (1 × 38)/ (2 × 9)
= (38/18)
= 19/9
=
(b) 5/8 of (i) (ii)
Solution:-
(i)
First convert the given mixed fraction into improper fraction.
=
Now,
= (5/8) × (23/6)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/8) × (23/6)
= (5 × 23)/ (8 × 6)
= (115/48)
=
(ii)
First convert the given mixed fraction into improper fraction.
=
Now,
= (5/8) × (29/3)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/8) × (29/3)
= (5 × 29)/ (8 × 3)
= (145/24)
=
8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed 2/5 of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
Solution:-
(i) From the question, it is given that,
Amount of water in the water bottle = 5 litres
Amount of water consumed by Vidya = 2/5 of 5 litres
= (2/5) × 5
= 2 liters
So, the total amount of water drank by Vidya is 2 litres
(ii) From the question, it is given that,
Amount of water in the water bottle = 5 litres
Then,
Amount of water consumed by Pratap = (1 – water consumed by Vidya)
= (1 – (2/5))
= (5-2)/5
= 3/5
∴ The total amount of water consumed by Pratap = 3/5 of 5 litres
= (3/5) × 5
= 3 liters
So, the total amount of water drank by Pratap is 3 litres
Exercise 2.3 Page: 41
1. Find:
(i) ¼ of (a) ¼ (b) 3/5 (c) 4/3
Solution:-
(a) ¼
We have,
= ¼ × ¼
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ¼ × ¼
= (1 × 1)/ (4 × 4)
= (1/16)
(b) 3/5
We have,
= ¼ × (3/5)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ¼ × (3/5)
= (1 × 3)/ (4 × 5)
= (3/20)
(c) (4/3)
We have,
= ¼ × (4/3)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ¼ × (4/3)
= (1 × 4)/ (4 × 3)
= (4/12)
= 1/3
(ii) 1/7 of (a) 2/9 (b) 6/5 (c) 3/10
Solution:-
(a) 2/9
We have,
= (1/7) × (2/9)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (1/7) × (2/9)
= (1 × 2)/ (7 × 9)
= (2/63)
(b) 6/5
We have,
= (1/7) × (6/5)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (1/7) × (6/5)
= (1 × 6)/ (7 × 5)
= (6/35)
(c) 3/10
We have,
= (1/7) × (3/10)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (1/7) × (3/10)
= (1 × 3)/ (7 × 10)
= (3/70)
2. Multiply and reduce to lowest form (if possible):
(i) (2/3) ×
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (2/3) × (8/3)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2 × 8)/ (3 × 3)
= (16/9)
=
(ii) (2/7) × (7/9)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2 × 7)/ (7 × 9)
= (2 × 1)/ (1 × 9)
= (2/9)
(iii) (3/8) × (6/4)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (3 × 6)/ (8 × 4)
= (3 × 3)/ (4 × 4)
= (9/16)
(iv) (9/5) × (3/5)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (9 × 3)/ (5 × 5)
= (27/25)
=
(v) (1/3) × (15/8)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (1 × 15)/ (3 × 8)
= (1 × 5)/ (1 × 8)
= (5/8)
(vi) (11/2) × (3/10)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (11 × 3)/ (2 × 10)
= (33/20)
=
(vii) (4/5) × (12/7)
Solution:-
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (4 × 12)/ (5 × 7)
= (48/35)
=
3. Multiply the following fractions:
(i) (2/5) × 5 ¼
Solution:-
First convert the given mixed fraction into improper fraction.
= 5 ¼ = 21/4
Now,
= (2/5) × (21/4)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2 × 21)/ (5 × 4)
= (1 × 21)/ (5 × 2)
= (21/10)
=
(ii) × (7/9)
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (32/5) × (7/9)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (32 × 7)/ (5 × 9)
= (224/45)
=
(iii) (3/2) ×
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (3/2) × (16/3)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (3 × 16)/ (2 × 3)
= (1 × 8)/ (1 × 1)
= 8
(iv) (5/6) ×
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (5/6) × (17/7)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5 × 17)/ (6 × 7)
= (85/42)
=
(v) × (4/7)
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (17/5) × (4/7)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (17 × 4)/ (5 × 7)
= (68/35)
=
(vi) × 3
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (13/5) × (3/1)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (13 × 3)/ (5 × 1)
= (39/5)
=
(vi) × (3/5)
Solution:-
First convert the given mixed fraction into improper fraction.
=
Now,
= (25/7) × (3/5)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (25 × 3)/ (7 × 5)
= (5 × 3)/ (7 × 1)
= (15/7)
=
4. Which is greater:
(i) (2/7) of (3/4) or (3/5) of (5/8)
Solution:-
We have,
= (2/7) × (3/4) and (3/5) × (5/8)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2/7) × (3/4)
= (2 × 3)/ (7 × 4)
= (1 × 3)/ (7 × 2)
= (3/14) … [i]
And,
= (3/5) × (5/8)
= (3 × 5)/ (5 × 8)
= (3 × 1)/ (1 × 8)
= (3/8) … [ii]
Now, convert [i] and [ii] into like fractions,
LCM of 14 and 8 is 56
Now, let us change each of the given fractions into an equivalent fraction having 56 as the denominator.[(3/14) × (4/4)] = (12/56) [(3/8) × (7/7)] = (21/56)
Clearly,
(12/56) < (21/56)
Hence,
(3/14) < (3/8)
(ii) (1/2) of (6/7) or (2/3) of (3/7)
Solution:-
We have,
= (1/2) × (6/7) and (2/3) × (3/7)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (1/2) × (6/7)
= (1 × 6)/ (2 × 7)
= (1 × 3)/ (1 × 7)
= (3/7) … [i]
And,
= (2/3) × (3/7)
= (2 × 3)/ (3 × 7)
= (2 × 1)/ (1 × 7)
= (2/7) … [ii]
By comparing [i] and [ii],
Clearly,
(3/7) > (2/7)
5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is ¾ m. Find the distance between the first and the last sapling.
Solution:-
From the question, it is given that,
The distance between two adjacent saplings = ¾ m
Number of saplings planted by Saili in a row = 4
Then, the number of gaps in saplings = ¾ × 4
= 3
∴The distance between the first and the last saplings = 3 × ¾
= (9/4) m
= 2 ¼ m
Hence, the distance between the first and the last saplings is 2 ¼ m.
6. Lipika reads a book for 1 ¾ hours every day. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
Solution:-
From the question, it is given that,
Lipika reads the book for = 1 ¾ hours every day = 7/4 hours
The number of days she took to read the entire book = was 6 days
∴Total number of hours required by her to complete the book = (7/4) × 6
= (7/2) × 3
= 21/2
= 10 ½ hours
Hence, the total number of hours she requires to complete the book is 10 ½ hours.
7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using 2 ¾ litres of petrol?
Solution:-
From the question, it is given that,
The total distance travelled by car in 1 litre of petrol = 16 km
Then,
Total quantity of petrol = 2 ¾ liter = 11/4 liters
Total number of distance travelled by car in 11/4 liters of petrol = (11/4) × 16
= 11 × 4
= 44 km
∴The total distance travelled by car in 11/4 litres of petrol is 44 km.
8. (a) (i) provide the number in the box [ ], such that (2/3) × [ ] = (10/30)
Solution:-
Let the required number be x,
Then,
= (2/3) × (x) = (10/30)
By cross multiplication,
= x = (10/30) × (3/2)
= x = (10 × 3) / (30 × 2)
= x = (5 × 1) / (10 × 1)
= x = 5/10
∴The required number in the box is (5/20)
(ii) The simplest form of the number obtained in [ ] is
Solution:-
The number in the box is 5/10
Then,
The simplest form of 5/10 is ½
(b) (i) Provide the number in the box [ ], such that (3/5) × [ ] = (24/75)
Solution:-
Let the required number be x,
Then,
= (3/5) × (x) = (24/75)
By cross multiplication,
= x = (24/75) × (5/3)
= x = (24 × 5) / (75 × 3)
= x = (8 × 1) / (15 × 1)
= x = 8/15
∴The required number in the box is (8/15)
(ii) The simplest form of the number obtained in [ ] is
Solution:-
The number in the box is 8/15
Then,
The simplest form of 8/15 is 8/15
Exercise 2.4 Page: 46
1. Find:
(i) 12 ÷ ¾
Solution:-
We have,
= 12 × reciprocal of ¾
= 12 × (4/3)
= 4 × 4
= 16
(ii) 14 ÷ (5/6)
Solution:-
We have,
= 14 × reciprocal of (5/6)
= 14 × (6/5)
= 84/5
(iii) 8 ÷ (7/3)
Solution:-
We have,
= 8 × reciprocal of (7/3)
= 8 × (3/7)
= (24/7)
(iv) 4 ÷ (8/3)
Solution:-
We have,
= 4 × reciprocal of (8/3)
= 4 × (3/8)
= 1 × (3/2)
= 3/2
(v) 3 ÷
Solution:-
While dividing a whole number by a mixed fraction, first convert the mixed fraction into an improper fraction
We have,
=
Then,
= 3 ÷ (7/3)
= 3 × reciprocal of (7/3)
= 3 × (3/7)
= 9/7
(vi) 5 ÷
Solution:-
While dividing a whole number by a mixed fraction, first convert the mixed fraction into an improper fraction
We have,
=
Then,
= 5 ÷ (25/7)
= 5 × reciprocal of (25/7)
= 5 × (7/25)
= 1 × (7/5)
= 7/5
2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.
(i) 3/7
Solution:-
Reciprocal of (3/7) is (7/3) [∵ ((3/7) × (7/3)) = 1]
So, it is an improper fraction.
An improper fraction is a fraction in which the numerator is greater than its denominator.
(ii) 5/8
Solution:-
Reciprocal of (5/8) is (8/5) [∵ ((5/8) × (8/5)) = 1]
So, it is an improper fraction.
An improper fraction is a fraction in which the numerator is greater than its denominator.
(iii) 9/7
Solution:-
Reciprocal of (9/7) is (7/9) [∵ ((9/7) × (7/9)) = 1]
So, it is a proper fraction.
A proper fraction is a fraction in which the denominator is greater than the numerator of the fraction.
(iv) 6/5
Solution:-
Reciprocal of (6/5) is (5/6) [∵ ((6/5) × (5/6)) = 1]
So, it is a proper fraction.
A proper fraction is a fraction in which the denominator is greater than the numerator of the fraction.
(v) 12/7
Solution:-
Reciprocal of (12/7) is (7/12) [∵ ((12/7) × (7/12)) = 1]
So, it is a proper fraction.
A proper fraction is a fraction in which the denominator is greater than the numerator of the fraction.
(vi) 1/8
Solution:-
Reciprocal of (1/8) is (8/1) or 8 [∵ ((1/8) × (8/1)) = 1]
So, it is a whole number.
Whole numbers are collections of all positive integers including 0.
(vii) 1/11
Solution:-
Reciprocal of (1/11) is (11/1) or 11 [∵ ((1/11) × (11/1)) = 1]
So, it is a whole number.
Whole numbers are collections of all positive integers including 0.
3. Find:
(i) (7/3) ÷ 2
Solution:-
We have,
= (7/3) × reciprocal of 2
= (7/3) × (1/2)
= (7 × 1) / (3 × 2)
= 7/6
=
(ii) (4/9) ÷ 5
Solution:-
We have,
= (4/9) × reciprocal of 5
= (4/9) × (1/5)
= (4 × 1) / (9 × 5)
= 4/45
(iii) (6/13) ÷ 7
Solution:-
We have,
= (6/13) × reciprocal of 7
= (6/13) × (1/7)
= (6 × 1) / (13 × 7)
= 6/91
(iv) ÷ 3
Solution:-
First convert the mixed fraction into improper fraction.
We have,
=
Then,
= (13/3) × reciprocal of 3
= (13/3) × (1/3)
= (13 × 1) / (3 × 3)
= 13/9
(iv) 3 ½ ÷ 4
Solution:-
First convert the mixed fraction into improper fraction.
We have,
= 3 ½ = 7/2
Then,
= (7/2) × reciprocal of 4
= (7/2) × (1/4)
= (7 × 1) / (2 × 4)
= 7/8
(iv) ÷ 7
Solution:-
First convert the mixed fraction into improper fraction.
We have,
=
Then,
= (31/7) × reciprocal of 7
= (31/7) × (1/7)
= (31 × 1) / (7 × 7)
= 31/49
4. Find:
(i) (2/5) ÷ (½)
Solution:-
We have,
= (2/5) × reciprocal of ½
= (2/5) × (2/1)
= (2 × 2) / (5 × 1)
= 4/5
(ii) (4/9) ÷ (2/3)
Solution:-
We have,
= (4/9) × reciprocal of (2/3)
= (4/9) × (3/2)
= (4 × 3) / (9 × 2)
= (2 × 1) / (3 × 1)
= 2/3
(iii) (3/7) ÷ (8/7)
Solution:-
We have,
= (3/7) × reciprocal of (8/7)
= (3/7) × (7/8)
= (3 × 7) / (7 × 8)
= (3 × 1) / (1 × 8)
= 3/8
(iv) ÷ (3/5)
Solution:-
First convert the mixed fraction into improper fraction.
We have,
=
Then,
= (7/3) × reciprocal of (3/5)
= (7/3) × (5/3)
= (7 × 5) / (3 × 3)
= 35/9
(v) 3 ½ ÷ (8/3)
Solution:-
First convert the mixed fraction into improper fraction.
We have,
= 3 ½ = 7/2
Then,
= (7/2) × reciprocal of (8/3)
= (7/2) × (3/8)
= (7 × 3) / (2 × 8)
= 21/16
(vi) (2/5) ÷ 1 ½
Solution:-
First convert the mixed fraction into improper fraction.
We have,
= 1 ½ = 3/2
Then,
= (2/5) × reciprocal of (3/2)
= (2/5) × (2/3)
= (2 × 2) / (5 × 3)
= 4/15
(vii) ÷
Solution:-
First convert the mixed fraction into improper fraction.
We have,
=
=
Then,
= (16/5) × reciprocal of (5/3)
= (16/5) × (3/5)
= (16 × 3) / (5 × 5)
= 48/25
(viii) ÷
Solution:-
First convert the mixed fraction into improper fraction.
We have,
=
=
Then,
= (11/5) × reciprocal of (6/5)
= (11/5) × (5/6)
= (11 × 5) / (5 × 6)
= (11 × 1) / (1 × 6)
= 11/6
Exercise 2.5 Page: 47
1. Which is greater?
(i) 0.5 or 0.05
Solution:-
By comparing whole numbers, 0 = 0
By comparing the tenth place digit, 5 > 0
∴ 0.5 > 0.05
(ii) 0.7 or 0.5
Solution:-
By comparing whole numbers, 0 = 0
By comparing the tenth place digit, 7 > 5
∴ 0.7 > 0.5
(iii) 7 or 0.7
Solution:-
By comparing whole numbers, 7 > 0
∴ 7 > 0.7
(iv) 1.37 or 1.49
Solution:-
By comparing whole numbers, 1 = 1
By comparing the tenth place digit, 3 < 4
∴ 1.37 < 1.49
(v) 2.03 or 2.30
Solution:-
By comparing whole numbers, 2 = 2
By comparing the tenth place digit, 0 < 3
∴ 2.03 < 2.30
(vi) 0.8 or 0.88
Solution:-
By comparing whole numbers, 0 = 0
By comparing the tenth place digit, 8 = 8
By comparing the hundredths place digit, 0 < 8
∴ 0.8 < 0.88
2. Express as rupees as decimals:
(i) 7 paise
Solution:-
We know that,
= ₹ 1 = 100 paise
= 1 paise = ₹ (1/100)
∴ 7 paise = ₹ (7/100)
= ₹ 0.07
(ii) 7 rupees 7 paise
Solution:-
We know that,
= ₹ 1 = 100 paise
= 1 paise = ₹ (1/100)
∴ 7 rupees 7 paise = ₹ 7 + ₹ (7/100)
= ₹ 7 + ₹ 0.07
= ₹ 7.07
(iii) 77 rupees 77 paise
Solution:-
We know that,
= ₹ 1 = 100 paise
= 1 paise = ₹ (1/100)
∴ 77 rupees 77 paise = ₹ 77 + ₹ (77/100)
= ₹ 77 + ₹ 0.77
= ₹ 77.77
(iv) 50 paise
Solution:-
We know that,
= ₹ 1 = 100 paise
= 1 paise = ₹ (1/100)
∴ 50 paise = ₹ (50/100)
= ₹ 0.50
(v) 235 paise
Solution:-
We know that,
= ₹ 1 = 100 paise
= 1 paise = ₹ (1/100)
∴ 235 paise = ₹ (235/100)
= ₹ 2.35
3. (i) Express 5 cm in meter and kilometer
Solution:-
We know that,
= 1 meter = 100 cm
Then,
= 1 cm = (1/100) m
= 5 cm = (5/100)
= 0.05 m
Now,
= 1 km = 1000 m
Then,
= 1 m = (1/1000) km
= 0.05 m = (0.05/1000)
= 0. 00005 km
(i) Express 35 mm in cm, m and km
Solution:-
We know that,
= 1 cm = 10 mm
Then,
= 1 mm = (1/10) cm
= 35 mm = (35/10) cm
= 3.5 cm
And,
= 1 meter = 100 cm
Then,
= 1 cm = (1/100) m
= 3.5 cm = (3.5/100) m
= (35/1000) m
= 0.035 m
Now,
= 1 km = 1000 m
Then,
= 1 m = (1/1000) km
= 0.035 m = (0.035/1000)
= 0. 000035 km
4. Express in kg:
(i) 200 g
Solution:-
We know that,
= 1 kg = 1000 g
Then,
= 1 g = (1/1000) kg
= 200 g = (200/1000) kg
= (2/10)
= 0.2 kg
(ii) 3470 g
Solution:-
We know that,
= 1 kg = 1000 g
Then,
= 1 g = (1/1000) kg
= 3470 g = (3470/1000) kg
= (3470/100)
= 3.470 kg
(ii) 4 kg 8 g
Solution:-
We know that,
= 1 kg = 1000 g
Then,
= 1 g = (1/1000) kg
= 4 kg 8 g = 4 kg + (8/1000) kg
= 4 kg + 0.008
= 4.008 kg
NCERT Solutions for Class 7 Maths Chapter 1 Integers
5. Write the following decimal numbers in the expanded form:
(i) 20.03
Solution:-
We have,
20.03 = (2 × 10) + (0 × 1) + (0 × (1/10)) + (3 × (1/100))
(ii) 2.03
Solution:-
We have,
2.03 = (2 × 1) + (0 × (1/10)) + (3 × (1/100))
(iii) 200.03
Solution:-
We have,
200.03 = (2 × 100) + (0 × 10) + (0 × 1) + (0 × (1/10)) + (3 × (1/100))
(iv) 2.034
Solution:-
We have,
2.034 = (2 × 1) + (0 × (1/10)) + (3 × (1/100)) + (4 × (1/1000))
6. Write the place value of 2 in the following decimal numbers:
(i) 2.56
Solution:-
From the question, we observe that,
The place value of 2 in 2.56 is one
(ii) 21.37
Solution:-
From the question, we observe that,
The place value of 2 in 21.37 is tens
(iii) 10.25
Solution:-
From the question, we observe that,
The place value of 2 in 10.25 is tenths.
(iv) 9.42
Solution:-
From the question, we observe that,
The place value of 2 in 9.42 is the hundredth.
(v) 63.352
Solution:-
From the question, we observe that,
The place value of 2 in 63.352 is the thousandth.
7. Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?

Solution:-
From the question, it is given that,
Distance travelled by Dinesh = AB + BC
= 7.5 + 12.7
= 20.2 km
∴ Dinesh travelled 20.2 km
Distance travelled by Ayub = AD + DC
= 9.3 + 11.8
= 21.1 km
∴Ayub travelled 21.1km
Clearly, Ayub travelled more distance by = (21.1 – 20.2)
= 0.9 km
∴Ayub travelled 0.9 km more than Dinesh.
8. Shyama bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
Solution:-
From the question, it is given that,
Fruits bought by Shyama = 5 kg 300 g
= 5 kg + (300/1000) kg
= 5 kg + 0.3 kg
= 5.3 kg
Fruits bought by Sarala = 4 kg 800 g + 4 kg 150 g
= (4 + (800/1000)) + (4 + (150/1000))
= (4 + 0.8) kg + (4 + .150) kg
= 4.8 kg + 4.150kg
= 8.950 kg
So, Sarala bought more fruits.
9. How much less is 28 km than 42.6 km?
Solution:-
Now, we have to find the difference between 42.6 km and 28 km
42.6
-28.0
14.6
∴ 14.6 km less is 28 km than 42.6 km.
Exercise 2.6 Page: 52
Find:
(i) 0.2 × 6
Solution:-
We have,
= (2/10) × 6
= (12/10)
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
Then,
= 1.2
(ii) 8 × 4.6
Solution:-
We have,
= (8) × (46/10)
= (368/10)
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
Then,
= 36.8
(iii) 2.71 × 5
Solution:-
We have,
= (271/100) × 5
= (1355/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 13.55
(iv) 20.1 × 4
Solution:-
We have,
= (201/10) × 4
= (804/10)
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
Then,
= 80.4
(v) 0.05 × 7
Solution:-
We have,
= (5/100) × 7
= (35/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 0.35
(vi) 211.02 × 4
Solution:-
We have,
= (21102/100) × 4
= (84408/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 844.08
(vii) 2 × 0.86
Solution:-
We have,
= (2) × (86/100)
= (172/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 1.72
2. Find the area of a rectangle whose length is 5.7cm and breadth is 3 cm.
Solution:-
From the question, it is given that,
Length of the rectangle = 5.7 cm
Breadth of the rectangle = 3 cm
Then,
Area of the rectangle = length × Breadth
= 5.7 × 3
= 17.1 cm2
3. Find:
(i) 1.3 × 10
Solution:-
On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
We have,
= 1.3 × 10 = 13
(ii) 36.8 × 10
Solution:-
On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
We have,
= 36.8 × 10 = 368
(iii) 153.7 × 10
Solution:-
On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
We have,
= 153.7 × 10 = 1537
(iv) 168.07 × 10
Solution:-
On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
We have,
= 168.07 × 10 = 1680.7
(v) 31.1 × 100
Solution:-
On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
We have,
= 31.1 × 100 = 3110
(vi) 156.1 × 100
Solution:-
On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
We have,
= 156.1 × 100 = 15610
(vii) 3.62 × 100
Solution:-
On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
We have,
= 3.62 × 100 = 362
(viii) 43.07 × 100
Solution:-
On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
We have,
= 43.07 × 100 = 4307
(ix) 0.5 × 10
Solution:-
On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
We have,
= 0.5 × 10 = 5
(x) 0.08 × 10
Solution:-
On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
We have,
= 0.08 × 10 = 0.8
(xi) 0.9 × 100
Solution:-
On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
We have,
= 0.9 × 100 = 90
(xii) 0.03 × 1000
Solution:-
On multiplying a decimal by 1000, the decimal point is shifted to the right by three places.
We have,
= 0.03 × 1000 = 30
4. A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?
Solution:-
From the question, it is given that,
Distance covered by two-wheeler in 1 litre of petrol = 55.3 km
Then,
Distance covered by two-wheeler in 10L of petrol = (10 × 55.3)
= 553 km
∴ The two-wheeler covers a distance of 553 km on 10L of petrol.
5. Find:
(i) 2.5 × 0.3
Solution:-
We have,
= (25/10) × (3/10)
= (75/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 0.75
(ii) 0.1 × 51.7
Solution:-
We have,
= (1/10) × (517/10)
= (517/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 5.17
(iii) 0.2 × 316.8
Solution:-
We have,
= (2/10) × (3168/10)
= (6336/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 63.36
(iv) 1.3 × 3.1
Solution:-
We have,
= (13/10) × (31/10)
= (403/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 4.03
(v) 0.5 × 0.05
Solution:-
We have,
= (5/10) × (5/100)
= (25/1000)
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
Then,
= 0.025
(vi) 11.2 × 0.15
Solution:-
We have,
= (112/10) × (15/100)
= (1680/1000)
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
Then,
= 1.680
(vii) 1.07 × 0.02
Solution:-
We have,
= (107/100) × (2/100)
= (214/10000)
On dividing a decimal by 10000, the decimal point is shifted to the left by four places.
Then,
= 0.0214
(viii) 10.05 × 1.05
Solution:-
We have,
= (1005/100) × (105/100)
= (105525/10000)
On dividing a decimal by 10000, the decimal point is shifted to the left by four places.
Then,
= 10.5525
(ix) 101.01 × 0.01
Solution:-
We have,
= (10101/100) × (1/100)
= (10101/10000)
On dividing a decimal by 10000, the decimal point is shifted to the left by four places.
Then,
= 1.0101
(x) 100.01 × 1.1
Solution:-
We have,
= (10001/100) × (11/10)
= (110011/1000)
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
Then,
= 110.011
Exercise 2.7 Page: 55
1. Find:
(i) 0.4 ÷ 2
Solution:-
We have,
= (4/10) ÷ 2
Then,
= (4/10) × (1/2)
= (2/10) × (1/1)
= (2/10)
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
Then,
= 0.2
(ii) 0.35 ÷ 5
Solution:-
We have,
= (35/100) ÷ 5
Then,
= (35/100) × (1/5)
= (7/100) × (1/1)
= (7/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 0.07
(iii) 2.48 ÷ 4
Solution:-
We have,
= (248/100) ÷ 4
Then,
= (248/100) × (1/4)
= (62/100) × (1/1)
= (62/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 0.62
(iv) 65.4 ÷ 6
Solution:-
We have,
= (654/10) ÷ 6
Then,
= (654/10) × (1/6)
= (109/10) × (1/1)
= (109/10)
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
Then,
= 10.9
(v) 651.2 ÷ 4
Solution:-
We have,
= (6512/10) ÷ 4
Then,
= (6512/10) × (1/4)
= (1628/10) × (1/1)
= (1628/10)
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
Then,
= 162.8
(vi) 14.49 ÷ 7
Solution:-
We have,
= (1449/100) ÷ 7
Then,
= (1449/100) × (1/7)
= (207/100) × (1/1)
= (207/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 2.07
(vii) 3.96 ÷ 4
Solution:-
We have,
= (396/100) ÷ 4
Then,
= (396/100) × (1/4)
= (99/100) × (1/1)
= (99/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 0.99
(viii) 0.80 ÷ 5
Solution:-
We have,
= (80/100) ÷ 5
Then,
= (80/100) × (1/5)
= (16/100) × (1/1)
= (16/100)
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
Then,
= 0.16
2. Find:
(i) 4.8 ÷ 10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 4.8 ÷ 10
= (4.8/10)
= 0.48
(ii) 52.5 ÷ 10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 52.5 ÷ 10
= (52.5/10)
= 5.25
(iii) 0.7 ÷ 10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 0.7 ÷ 10
= (0.7/10)
= 0.07
(iv) 33.1 ÷ 10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 33.1 ÷ 10
= (33.1/10)
= 3.31
(v) 272.23 ÷ 10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 272.23 ÷ 10
= (272.23/10)
= 27.223
(vi) 0.56 ÷ 10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 0.56 ÷ 10
= (0.56/10)
= 0.056
(vii) 3.97 ÷10
Solution:-
On dividing a decimal by 10, the decimal point is shifted to the left by one place.
We have,
= 3.97 ÷ 10
= (3.97/10)
= 0.397
3. Find:
(i) 2.7 ÷ 100
Solution:-
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
We have,
= 2.7 ÷ 100
= (2.7/100)
= 0.027
(ii) 0.3 ÷ 100
Solution:-
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
We have,
= 0.3 ÷ 100
= (0.3/100)
= 0.003
(iii) 0.78 ÷ 100
Solution:-
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
We have,
= 0.78 ÷ 100
= (0.78/100)
= 0.0078
(iv) 432.6 ÷ 100
Solution:-
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
We have,
= 432.6 ÷ 100
= (432.6/100)
= 4.326
(v) 23.6 ÷100
Solution:-
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
We have,
= 23.6 ÷ 100
= (23.6/100)
= 0.236
(vi) 98.53 ÷ 100
Solution:-
On dividing a decimal by 100, the decimal point is shifted to the left by two places.
We have,
= 98.53 ÷ 100
= (98.53/100)
= 0.9853
“UNRAVELING THE FURY OF NATURE: UNDERSTANDING TORNADO”
4. Find:
(i) 7.9 ÷ 1000
Solution:-
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
We have,
= 7.9 ÷ 1000
= (7.9/1000)
= 0.0079
(ii) 26.3 ÷ 1000
Solution:-
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
We have,
= 26.3 ÷ 1000
= (26.3/1000)
= 0.0263
(iii) 38.53 ÷ 1000
Solution:-
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
We have,
= 38.53 ÷ 1000
= (38.53/1000)
= 0.03853
(iv) 128.9 ÷ 1000
Solution:-
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
We have,
= 128.9 ÷ 1000
= (128.9/1000)
= 0.1289
(v) 0.5 ÷ 1000
Solution:-
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
We have,
= 0.5 ÷ 1000
= (0.5/1000)
= 0.0005
5. Find:
(i) 7 ÷ 3.5
Solution:-
We have,
= 7 ÷ (35/10)
= 7 × (10/35)
= 1 × (10/5)
= 2
(ii) 36 ÷ 0.2
Solution:-
We have,
= 36 ÷ (2/10)
= 36 × (10/2)
= 18 × 10
= 180
(iii) 3.25 ÷ 0.5
Solution:-
We have,
= (325/100) ÷ (5/10)
= (325/100) × (10/5)
= (325 × 10)/ (100 × 5)
= (65 × 1)/ (10 × 1)
= 65/10
= 6.5
(iv) 30.94 ÷ 0.7
Solution:-
We have,
= (3094/100) ÷ (7/10)
= (3094/100) × (10/7)
= (3094 × 10)/ (100 × 7)
= (442 × 1)/ (10 × 1)
= 442/10
= 44.2
(v) 0.5 ÷ 0.25
Solution:-
We have,
= (5/10) ÷ (25/100)
= (5/10) × (100/25)
= (5 × 100)/ (10 × 25)
= (1 × 10)/ (1 × 5)
= 10/5
= 2
(vi) 7.75 ÷ 0.25
Solution:-
We have,
= (775/100) ÷ (25/100)
= (775/100) × (100/25)
= (775 × 100)/ (100 × 25)
= (155 × 1)/ (1 × 5)
= (31 × 1)/ (1 × 1)
= 31
(vii) 76.5 ÷ 0.15
Solution:-
We have,
= (765/10) ÷ (15/100)
= (765/10) × (100/15)
= (765 × 100)/ (10 × 15)
= (51 × 10)/ (1 × 1)
= 510
(viii) 37.8 ÷ 1.4
Solution:-
We have,
= (378/10) ÷ (14/10)
= (378/10) × (10/14)
= (378 × 10)/ (10 × 14)
= (27 × 1)/ (1 × 1)
= 27
(ix) 2.73 ÷ 1.3
Solution:-
We have,
= (273/100) ÷ (13/10)
= (273/100) × (10/13)
= (273 × 10)/ (100 × 13)
= (21 × 1)/ (10 × 1)
= 21/10
= 2.1
6. A vehicle covers a distance of 43.2 km in 2.4 litres of petrol. How much distance will it cover in one litre of petrol?
Solution:-
From the question, it is given that,
Total distance covered by vehicle in 2.4 litres of petrol = 43.2 km
Then,
Distance covered in 1 litre of petrol = 43.2 ÷ 2.4
= (432/10) ÷ (24/10)
= (432/10) × (10/24)
= (432 × 10)/ (10 × 24)
= (36 × 1)/ (1 × 2)
= (18 × 1)/ (1 × 1)
= 18 km
∴ The total distance covered in 1 litre of petrol is 18 km.



































